Кинематика
- Вектор перемещения
- Прямолинейное равномерное движение
- Неравномерное движение
- Мгновенная скорость
- Ускорение
- Свободное падение
- Движение тела, брошенного горизонтально или под углом к горизонту
- Относительность механического движения
- Криволинейное движение
- Равномерное движение по окружности
- Центростремительное ускорение
- Равнопеременное движение по окружности
Статика
МЕХАНИКА
МКТ
ЭЛЕКТРОДИНАМИКА
ОПТИКА
Центростремительное ускорение. | |
|
Вычислим величину ускорения при равномерном
движении точки по окружности и найдем его направление. Пусть за некоторый промежуток времени t тело переместилось из точки А в точку А1 с постоянной по модулю скоростью. Изобразим вектора скорости в этих точках и найдем вектор изменения скорости 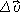 Рассмотрим треугольники АА1О и А1CB. Эти треугольники равнобедренные и углы при их вершинах равны, т.к. 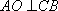 и и 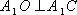 (углы со взаимно перпендикулярными сторонами). Следовательно, эти
треугольники подобны.
(углы со взаимно перпендикулярными сторонами). Следовательно, эти
треугольники подобны. |
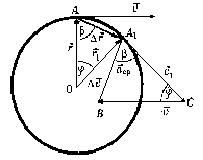 |
Из подобия треугольников следует пропорция:
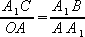 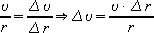 |
Примеры:
|
Разделим правую и левую части
равенства на промежуток времени, за которое совершено перемещение, и учтем,
что
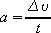 и и 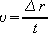 Тогда 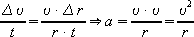 |
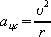 |
Теперь определим направление ускорения. Т.к. мы
должны для определения ускорения брать предел при 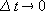 ,
то из рисунка видно, что угол ,
то из рисунка видно, что угол 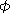 будет уменьшаться (
будет уменьшаться (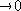 ),
а ),
а 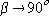 . .Это значит, что прямая А1В (вектор 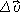 )
будет стремиться наложиться на АО. Но вектор ускорения
сонаправлен с вектором изменения скорости. )
будет стремиться наложиться на АО. Но вектор ускорения
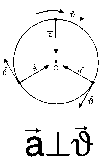
сонаправлен с вектором изменения скорости. Следовательно, вектор ускорения при равномерном движении по окружности направлен к центру окружности (центру вращения). Поэтому ускорение наз. центростремительным ускорением. |
|
|
Центростремительное ускорение меняет скорость
только по направлению, но не меняет по величине.
Вектор центростремительного ускорения перпендикулярен вектору скорости. Используя связь между угловой и линейной скоростями, получим: 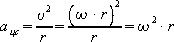 |
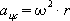 |